What Is X-Ray Diffraction?

X-ray diffraction (XRD) is a non-destructive method that lets you calculate the interplanar spacing of the atoms within a solid using Bragg’s Law.

There are numerous applications for XRD, including measuring residual stress on the surface of a material by pointing X-rays towards a polycrystalline solid and measuring the return X-ray scatter that constructively interferes as it bounces off the object.

In this article, we’ll cover some of the different XRD measurement techniques, common applications of XRD in the real world, and explore in detail how XRD can be used to measure residual stresses of polycrystalline solids.

What Is the Principle of X-ray Diffraction?

X-ray diffraction is used to identify a crystal’s atomic and molecular structure. The X-ray pattern contains information about the spacing of the lattice planes and crystal orientation, which is used to determine the crystal’s structure. The fundamental principle of X-ray diffraction is Bragg’s Law, which we’ll cover later in this article.

XRD Techniques

X-ray diffraction can be performed using various techniques depending on the application and the particular use case where it’s being implemented. These techniques include the Sin2 ψ method, the Two-Angle method, the Marion-Cohen method, and the cosα method.

sin2 ψ

The sin2 ψ method was initially developed in the 1920s and used for X-ray residual stress analysis for many decades; this method is also still used by manufacturers today.

To perform a measurement using sin2 ψ, a zero or one-dimensional sensor is used to acquire a portion of the diffraction Debye-Scherrer ring. Once a portion of the ring has been acquired, the incidence angle is changed to acquire the remaining crystal distortion data. Debye-Scherrer rings are the resulting concentric diffraction rings produced by Bragg reflections when a highly parallel electron beam illuminates polycrystalline grains within an object.

Two-Angle

Just as the name suggests, the two-angle method is used to determine stress within a polycrystalline material by measuring the lattice spacing of any two ψ (psi) angles, as long as the lattice spacing is a linear function of sin2 ψ. Lattice spacing data is then determined by using two extreme values of ψ, typically 0 and 45 degrees.

Marion-Cohen

The Marion-Cohen method can be used to measure residual stresses within an object by characterizing the dependence of lattice spacing on stresses within highly textured materials. 

For stresses produced by shot peening, machining, or grinding, residual stresses that are measured with the Marion-Cohen method produce nearly identical results when compared to the Two-Angle and sin2 ψ methods.

cosα

The cosα (cosine alpha) XRD method is an improvement on the sin2 ψ (sin squared psi) method we discussed earlier.

Instead of using a zero or one-dimensional sensor, this technique utilizes a two-dimensional sensor to acquire the entire Debye-Scherrer ring simultaneously. Due to this single-exposure measurement, changing the angle of incidence is no longer necessary, and a goniometer is no longer required in the XRD measurement device.

Is XRD the Same as XRF?

No, XRD (X-ray diffraction) is not the same as XRF (X-ray fluorescence), even though both methods are sometimes used together to analyze a particular material or sample.

While XRD is used to measure and identify the mineralogy of an object, XRF gives information about the sample’s chemical composition, such as the types of elements present. XRF does not provide the exact composition and molecular structure of the sample, such as that provided by XRD.

Common XRD Applications

There are many different applications for XRD, with one of the most common being the measurement of residual stresses within polycrystalline solids.

Some of the most common XRD applications include:

• Determining Structural Properties of Materials
  • Grain Size
  • Strain
  • Lattice Parameters
  • Phase Composition
  • Preferred Orientation
  • Epitaxy
• Identifying Orientation & Crystalline Phases
• Determining Atomic Arrangement
• Measuring Multi-Layers & Thickness of Thin Films
• Determining Unit Cell Dimensions
• Measuring Sample Purity
• Determining Modal Amounts of Minerals

How Does XRD Measure Residual Stress?

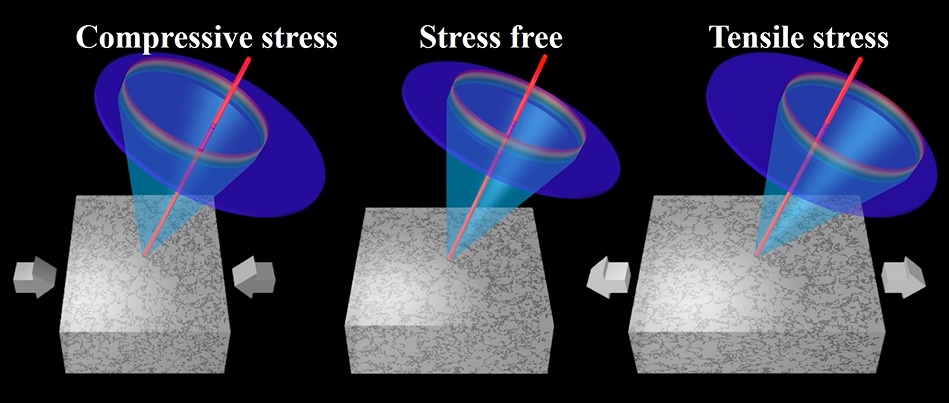
XRD doesn’t measure residual stress, per se, but it gives the information and data required to calculate residual stresses and strains within an object.

By using the various XRD techniques mentioned above, you can observe peak profiles in select sections of the Debye-Scherrer rings.

How Do You Calculate Stress from XRD Data?

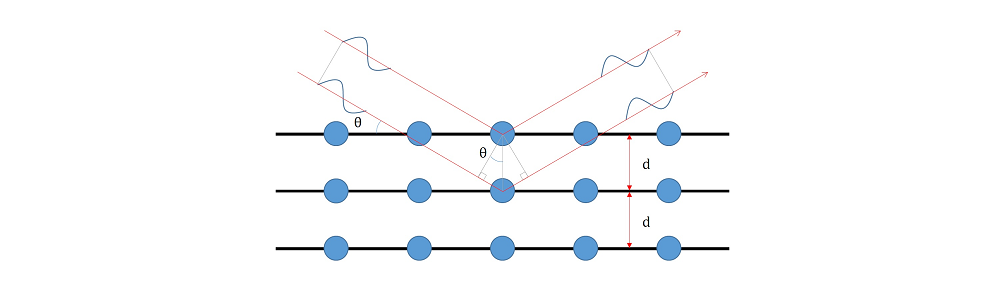
Stresses are calculated from XRD using a fundamental physics principle called Bragg’s Law. This law states that every atomic plane within a crystalline structure undergoes refraction at one unique angle for any number of X-rays of a fixed wavelength.

This means you can use the incident ray, wavelength, and a measurement angle theta to solve Bragg’s equation and determine the d-spacing between the crystal lattice planes of atoms in a polycrystalline material. Once you know the d-spacing, you can compare a nominal unstressed sample to a stressed sample in order to determine the precise stresses present.

Advantages of XRD

One of the biggest advantages of XRD is the fact that it is a non-destructive measurement method, meaning that your test sample is fully preserved before and after the technique. Additionally, it’s easy to calculate residual stresses using XRD data, and simple to interpret the data that the X-ray diffraction method provides. Spotting X-ray to some millimeter area on a sample, it’s possible to obtain a wide range of structural properties incredibly quickly.

Have Questions About X-Ray Diffraction & Residual Stress Measurement?

Pulstec is a leader in the residual stress measurement device space and has developed a cutting-edge XRD residual stress analyzer that is used by manufacturers and R&D departments all over the globe.

If you have questions about X-ray diffraction, or would like to request a free demo of our XRD analyzer, contact us today.